まず普通の輪ゴム（１）を用意します。この輪ゴムを
（＊）曲げたり伸ばしたりしながら空間の中で連続的に変形して
　 （決してハサミで切ってあとで張り合わせたりせずに！）
右の輪ゴム（２）に重ね合わせることが可能かどうかを考えてみましょう。

（１）の輪ゴムは　（１−１）の輪ゴムには変形可能です。
その変形の仕方は次のようになります。

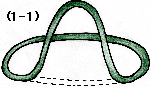
実は（１）の輪ゴムは（２）には（＊）の操作ではどのように変形させても重ね合わせることが出来ないのです。
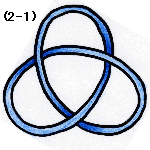
次に（３）の輪ゴムを考えてみます。これも（＊）の操作では（１）にも（２）にも 重ね合わせることが出来ません。

（１）の輪ゴムは自明な結び目といいます。つまり自明であるとは, 結び目がないことを意味します。それに反して，例えば（２）や（３）はどこをどのように伸び縮みさせても結び目が出来てしまうことはお分かりでしょう。

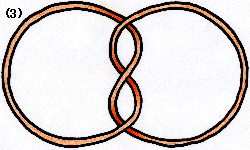
では（２）と（２−１）はどうでしょうか？
これらは一見すると，とても良く似ています。輪ゴムの弧の上下関係が異なっているだけです。（２）を鏡に映すと（２−１）が鏡の中に見えるでしょう。実はこれも（＊）の操作では重ね合わせる事が出来ません。

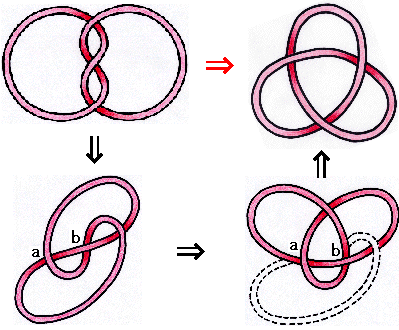
また，（２）と（３）は一見かなり違って見えますが，次の図のように実は（＊）の操作で重ね合わせる事が出来ます。

いろいろな結び目を具体的に作ってみたい人は, 例えば次の方法があります。タイヤチューブを用意して下に描いてある線に沿って切り取ると（１）や（２）が出来る事はお分かりでしょう。

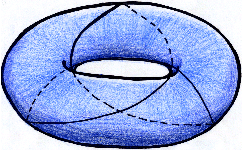
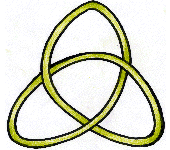
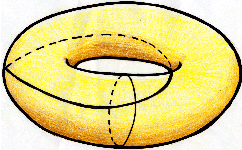
空間の次元をひとつ上げて４次元空間内の結び目を考えると，ひとつ余分にある次元を利用して，どんな結び目も自明な結び目に変形できます。ですから我々の住んでいる３次元空間というのは，ずいぶん豊かな構造をしているとも言えます。これに関連して３次元多様体論が現在進行形で研究されています。

すると（＊）の操作で重ね合わせる事が出来るものとそうでないものは，どれ位あるか分類してみようという問題が出て来ます。このようなことを研究するのが位相幾何学の「結び目理論」といわれている数学のひとつの分野で, 現在盛んに研究されています。

　上にあげた例は全て結び目が有限個のものでしたが，次の例のように，無限個の結び目をもつものがありますので，一口に「結び目理論」といってもなかなか奥が深いものです。

　また，普通の意味での結び目，つまり２本のひもを結んで一本の長いひもを作る結び方についてももちろん研究されています。簡単な結び方を３つ描いておきます。参考文献[1]

　色々な天体の動きや人工衛星の軌道も全て結び目です。なぜこのような問題を研究するのか？といえば，第一には数学的に大変興味深い研究対象であり，現在盛んに研究されている３次元多様体の理論に直接結びついていること。第二には物理やDNAへの応用があること等をあげることができます。参考文献[2],[3]

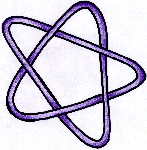
　このように古くからある数学の問題が，現在研究されている科学に直接関連を持っているということは，数学が学問の中で普遍的な真理を追求していることの現れであるといえます。数学好きの人は，広い視野を持って勉強して，我々の住んでいる空間そのものがどのような構造になっているかを探求してみませんか？

　最後に結び目関連のホームページの例をあげておきます。