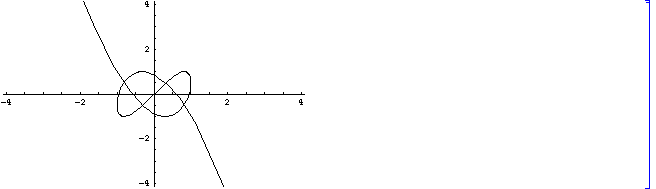
part II
さて、(IV) リサジュ曲線で紹介した曲線のうち、
(iv) x= Sin[3 t], y=Sin[5 t]
(vi) x=Sin[5 t], y=Sin[7 t]
(vii) x=Sin[5 t], y=Sin[7 t]
などは曲線が途中で途切れているとの印象を受けます。
例えば、(iv) について考えてみよう。
Sin[3 t] = -4 (Sin[t])^3 +3 Sin[t],
Sin[5 t]= 16 (Sin[t])^5 -20 (Sin[t])^3 + 5 Sin[t]
であるから、上で描いた曲線は、
x= -4 s^3 +3 s, y= 16 s^5 -20 s +5 s (-1 < s < 1)
を描いたことになります。ここで、s を -1 から +1まで動かすという制約をとり払えば、
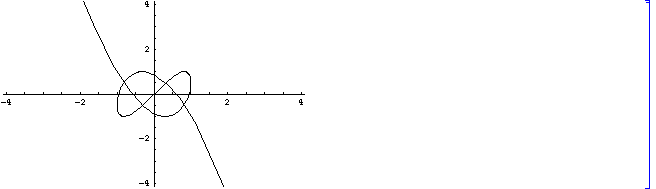
という(ような)曲線となります。この曲線は、長さが有限の辺をもつ長方形のなかにはおさまらないので、その部分をここでは描いています。 xと y は、
16 x^5 -20 x^3 +5 x +4 y^3 -3 y = 0
という関係式を満たします。
第(V)章 これまで考えてきた曲線をもう少し一般化して、x, yがともに、Cos[t], Sin[t]
の有理関数で表わされ、 Tan[s]= y/x なる変数 s を用いて
r = Sqrt[ x^2 +y^2] または r^2 =x^2 +y^2 が、Cos[s], Sin[s]
または、有理数 a > 0 に対する Cos[a s], Sin[a s]の多項式としてあらわ
されるものを考えよう。
(i) まず、Lemniscate , レムニスケート, 連珠形
(ベルヌーイのレムニスケート、 lemniscate ofBernoulli )
x = Cos[t]/(1 +(Sin[t])^2 ),
y= Sin[t] Cos[t]/(1 +(Sin[t])^2)
( 0 < t < 2 Pi)
を眺めてみよう。
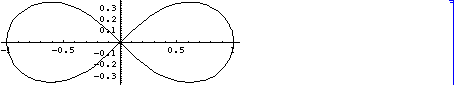
( cf. リマソンについての教科書の記述、
永尾 汎 ほか ”数学 C”
(数研出版)pp. 92, 演習問題 17. )
上記のような媒介変数表示のとき、
y/x = Sin[t]
だから x =R Cos[s], y = R Sin[s]
とすれば、y^2/x^2 = (Tan[s])^2 であり、
r^2= x^2 +y^2 = ((Cos[t])^2 +(Sin[t])^2 (Cos[t])^2)/(1+(Sin[t])^2)^2
=Cos[t]^2/(1 +(Sin[t])^2) =(1 -(Sin[t])^2)/(1+(Sin[t])^2)
=(1 -y^2/x^2)/(1 +y^2/x^2)=( 1 -(Tan[s])^2)/(1 +(Tan[s])^2)
=2 Cos[s]^2 -1 =Cos[2 s] となる。
x, y は、次のような方程式を満たす
(x^2 +y^2)^2 -(x^2 -y^2) = 0
この方程式を ”同次化” すると、
X^4 +2 X^2 Y^2 +Y^4 - X^2 Z^2 + Y^2 Z^2 =0
という方程式が得られます。この曲線を”複素射影代数曲線”として扱うと、
(x, y)=(0, 0) 即ち (X, Y, Z)=(0, 0, 1)なる点 と 無限遠点でしかも虚の点
(X, Y, Z)= (1, i, 0) および (X, Y, Z)=(1, -i, 0) の3点で 通常2重点を持ちます。
また、 この曲線は、リサジュ曲線を扱ったときに登場した
x= Sin [t], y= Sin[2 t] ( 0 < t < 2 Pi )
という曲線と見かけの上でかなり似ています。こちらの方は方程式
4 x^4 -4 x^2 + y^2 =0
をみたし、さらにこれを ”同次化” すると、
4 X^4 - 4 X^2 Z^2 +Y^2 Z^2 = 0
を満たします。この曲線を、”複素射影代数曲線”として扱うと、
(x, y)=(0,0) 即ち (X, Y, Z)=(0,0,1) で 通常2重点をもち、
(X, Y, Z)= (0, 1, 0)なる無限遠点で接触結節点を持ちます。 この点の近くでの
曲線の状況を見よう。 Y=1, X=x, Z=i z と置き非同次の方程式
4 x^4 + 4 x^2 z^2 - z^2 =0
を考える。このとき、 z = 2 x^2 / Sqrt[1 -4 x^2], z=- 2 x^2/Sqrt[1- 4 x^2]
が得られる。これを描くと次のようになります。
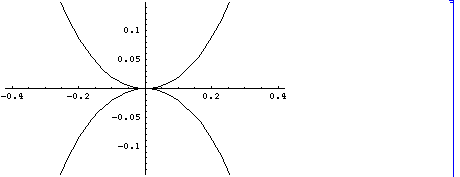
これらの考察で、レムニスケートと リサジュの m=1, n=2の場合が本質的に異なる性質をもつことがわかる。m=1, n=2のリサジュの方は、 8の字曲線 the figure 8 curve
とか、Geromoのレムニスケート the lemniscate of Geromo という名前が
付いていま
す。(cf. A. Gray " Modern Differential Geometry of Curves andSurface ",
CRC Press, pages 21-22). 弘前大学の入試問題の過去問題を勉強した人は、この8の字
曲線に関する問題が平成10年度入学者の入試前期日程(1998年2月実施)の数学 III 問
題 11 に出ているのがわかると思います。
”複素射影代数曲線” とみて、4次の既約代数曲線で、1個の
う意味では8の字曲線の仲間です。
(x^2 +y^2 -3 x)^2 -4 x^2 (2 -x)
= x^2 -2 x^3 +x^4 -6 x y^2 +2 x^2 y^2 +y^4 = 0
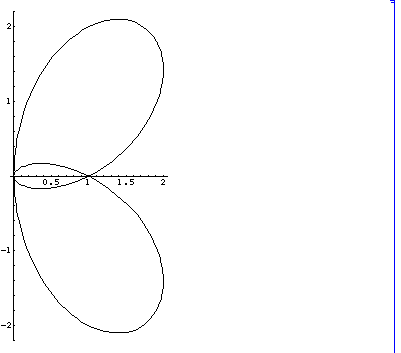
(ii) 次に パスカルのリマソン Limacon
x=(2 Cos[t] +1) Cos[t],
y=( 2 Cos[t] +1) Sin[t]
( 0 < t < 2 Pi)
を眺めてみよう。

この曲線は、
(x^2 +y^2 -2 x)^2 -(x^2 +y^2)
=3 x^2 -4 x^3 +x^4 -y^2 -4 x y^2 +2 x^2 y^2 +y^4 =0
という方程式を満たす。 r = 2 Cos[t] +1.
”複素射影代数曲線”としてこの曲線をみて、同次方程式
(X^2 +Y^2 -2 X Z)^2 -X^2 Z^2 -Y^2 Z^2 = 0
を考える。リマソンは、 (x, y)=(0, 0) 即ち (X, Y, Z)=(0, 0, 1)に通常2重点を持ちま
す。また、虚の無限遠点 (X, Y, Z)=(1, i, 0) および、(X, Y, Z)=(1,-i, 0) において単純尖
点を持ちます。さらに、上で考えた曲線を一般化さひて、1 よりより大きい b に対
し、 r =b Cos[t] +1 即ち
x =(b Cos[t] +1) Cos[t], y= (b Cos[t] +1) Sin[t]
( 0 < t < 2 Pi) とすれば、この曲線は、方程式
x^4 +2 x^2 y^2 +y^4 +(b^2 -1) x^2 -2 b x^3 -y^2 -2 b x y^2
= (x^2 +y^2 -b x)^2 -(x^2 +y^2) = 0
を満たし、”複素射影代数曲線” (X^2 +Y^2 -b X Z) -(X^2 +Y^2) Z^2=0 は、
(X, Y, Z)=(0, 0, 1) で通常2重点を、 (X, Y, Z)=(1, i, 0) および(X, Y, Z)=(1, -i, 0)
で、単純尖点を持ちます。b=2の場合に、この単純尖点を見てみましょう。
X=1, Z =z, Y=i y として、z 軸を横軸、 y軸を縦軸にとって 曲線
y^4 +y^2 z^2 +4 y^2 z -2 y^2 +3 z^2 -4 z +1 = 0
を描きますと、次のようになります。

代数曲線論の立場からは、リマソンは、その双対曲線がリマソンと(射影的に)同形で
あるという性質が注目されます。
(ii) ”数学 C”でよく取り上げられる曲線の別の例として、
x = Sin[ a t] Cos[t] =(1/2) ( Sin[ (a +1) t] +Sin[ (a-1) t])
y= Sin[a t] Sin[t] = (1/2) (- Cos[(a+1) t] +Cos[ (a-1) t])
があります。ここで、 a > 0 は、正 の有理数とします。
a=3 の場合は、次のような曲線となります。
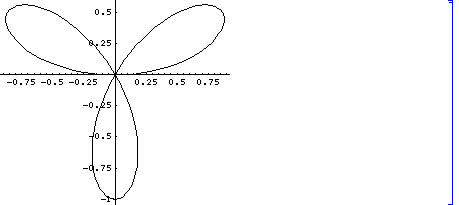
この曲線は、
(x^2 +y^2)^2 +y ( y^2 -3 x^2) = 0
という方程式を満たします。
END