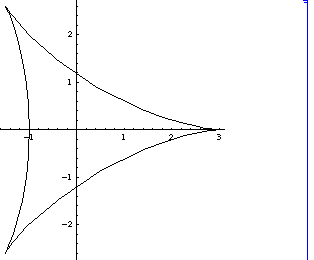
　　　　数理システム科学科　数理システム解析講座提供　Home Page　

　　　　曲線を眺める　

　 ....... 1998 Autumn

　数理科学では、さまざまな曲線を扱いますが、まず高校の数学C　などに登場するおなじみ

の曲線やそれをちょっと一般化した曲線を眺めてみましょう。

　　ここで、取り上げるのは、平面代数曲線　のうちで、

　　　　　　　有理曲線　と呼ばれているものです。

　　　x座標、　y座標　ともに　１つの媒介変数　sの有理関数で媒介変数表示される：

　　　　x= x(s), y= y(s)　のがこのような曲線の特徴です。　ここで、x(s), y(s) は、

　　　　変数　s についての有理関数とします。

目次　： Contents　

　　第(I)章　Hypocycloid 　ハイポサイクロイド　

　　　　　　　　　　　　　　３個の図

　　第(II)章　Epicycloid　エピサイクロイド

　　　　　　　　　　　　　　４個の図

　　第(III)章　偶数次 (n=2m 次）の代数曲線で、 (n-1) (n -2)/2=(m-1) (2 m -1)

　　　　個の　２重点を持つもの　

　　　　　　　　　　　　　　７個の図

　　第(IV)章　 Lissajou リサジュ曲線　

　　　　　　　　　　　　　　１１個の図　

　　第(V)章　 r = f (theta) 　と表示される　有理曲線

　　　　　　　　　　　　　　６個の図　

　　第(VI)章　補論　射影幾何学の古典的定理の紹介

　ここで、紹介する曲線は、かなり有名なものが大半ですが、(III)でとりあげる曲線は、

　ルーレット曲線ではあるものの、”双曲的”多項式の研究との関連より登場した、いくらか

　オリジナリティのある曲線です。

　[ このHome Page では、数式　がいろいろと登場します。　

　　　　　　不等号　 <　は、　

　　　等号付きの不等号の意味で使っています。

　すなわち、　a < x < b は、x を　a から　bまで、動かすことを意味し、このとき、　a や　bも含まれます。 ] 　　

第(I)章　　曲線その１：　Hypocycloid 　ハイポサイクロイド　

　　　　　x = n Cos[t] + Cos[n t] ,

　　　　　y=n Sin[t] - Sin[n t]

　　　　　　　( 0 < t < 2 Pi )

　　　　　[ n = 2, 3, 4, ....... ]

(1) n= 2 , Deltoid デルトイド, シュタイナーのハイポサイクロイド、

　　 the three-cusped hypocycloid, the Steiner hypocycloid

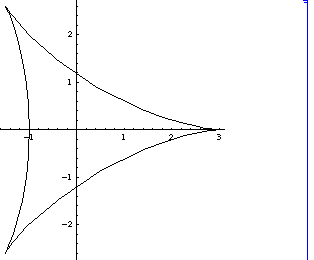
　(2) n=3, Astroid アストロイド、　星ぼう形、star curve,

　[ぼう　....草かんむり　の下に　亡　と書いてできる漢字です]

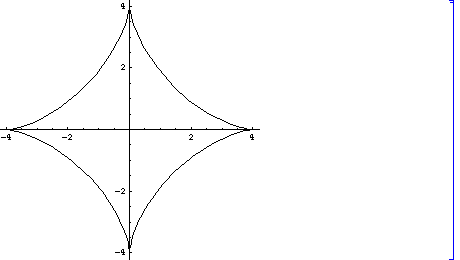
x/4 = (3 Cos[t] + Cos[3 t])/4=(3 Cos[t] +4 (Cos[t])³ -3Cos[t])/4=(Cos[t])³

y/4 =(3 Sin[t] -Sin[3t])/4 =(3 Sin[t] +4 (Sin[t])³-3Sin[t])/4 =(Sin[t])³

　ゆえに (x/4)^(2/3) +(y/4)^(2/3)=1が成り立ちます。

　　　　cf. 山本芳彦　編　”数学 C”　（啓林館）p. 205

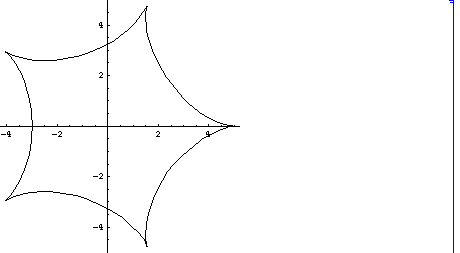
(3) n=4 ,

第(II)章　曲線その2： Epicycloid　エピサイクロイド

　　　　　x = n Cos[t] - Cos[n t] ,

　　　　　y= n Sin[t] - Sin[n t]

　 ( 0 < t < 2 Pi )

[ n = 2, 3, 4, ....... ]

　(1) n=2, Cardioid, カージオイド、心臓形　heartcurve,

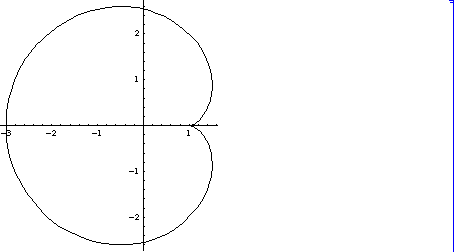
　この曲線を　軸方向に　-1 ずらすと、

　　　 x₁= 2 Cos[t] - Cos[2 t] -1 = -(2 (Cos[t])² -1) -1 +2 Cos[t]

　　　　　　=Cos[t] ( 2 -2 Cos[t] )

　　　y₁=2 Sin[t] -Sin[2t] =Sin[t] (2 -2 Cos[t]).

ここで、t =Pi -s とすれば、　x₁=- Cos[s] (2 +2 Cos[s]),

　　　　y₁= Sin[s] (2 +2 Cos[s])

だから、この曲線　x₁(s), y₁(s) を　y軸に関して裏返したものを、極座標で

　　r =2 +2 Cos[s] 即ち、　

　　x= (2 +2 Cos[s]) Cos[s], y=(2 +2 Cos[s]) Sin[s]

(0 < s < 2 Pi) と表わすことができます。

cf. 　(i) 永尾　汎　ほか　”数学 C”

　　　　（数研出版）pp. 86-87, pp. 90

　　　(ii)　藤田宏、前原昭二　編 ”数学 C"

　　(東京書籍) p. 88

(2) n=3, Nephroid, ネフロイド、腎臓形　,kidney curve

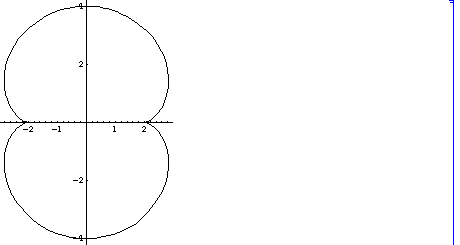
上図のようなネフロイドの（例えば）右半分即ち　x > 0なる部分は、次のような

　古典的な光学の問題の解となっています。このような問題は、Brieskornという人他

　１名の本[あとで書名を紹介します]の31頁によれば、ホイヘンス　Huygensの

　 ”光学”　"Traite de la lumiere" [1690 年] に出ています。

　　　　鏡の面[線]が

　　　X= 4 Cos[s], Y=Sin[s] ( -Pi/2 < s < Pi/2)　というかっこうであったとき、

　左から右へ x軸に平行な光の束が進入し、この鏡で反射してできる反射光よりなる（半）

直線の１径数族の包絡線となります。この包絡線を、火線　causticと言います。

Image 764. gif

[ caustic.nb]

　(3) n=4

(4) n=5

[[ 考察]] 第(I)章と第(II)章　でとりあげた曲線の媒介変数表示において、

　複素形　z= z(t)= x(t) +i y(t) を考えてみれば、　

　　　ハイポサイクロイドは、　　z(t)= n Exp[i t] + Exp[-i n t]

という式を、また　

　　　エピサイクロイドは、　 z(t)=n Exp[i t] - Exp[ -i n t]

という式をしています。　

　　さて、Egbert Brieskorn, Horst Knoerrer (ボン大学）著の

　”平面代数曲線”　( " Plane Algebraic Curves",1986年、バークホイザー

Birkhaeuser ; 原著　ドイツ語版　Ebene algebraische Kurven )

の　２６頁にハイポサイクロイドやエピサイクロイドが著名な数学者によって研究された

　時期がかかれてあります。

　　　　 Daniel Bernpulli ダニエル　ベルヌーイ　1725年

　　　　Jacob Bernoulli ヤコブ　ベルヌーイ　1692-1699年

　　　　 Johann Bernoulli ヨハン　ベルヌーイ　1695年

　　　　Desargues デザルグ　　1593-1662 年 [?]

　　　　Albrecht Duerer デューラー（画家）　1525年

　　　　Euler オイラー　　1745年、1781年

　　　　de la Hire 1694 年

　　　　l'Hospital ロピタル　1661-1704年

　　　　Huygens ホイヘンス　1679年

　　　　Newton ニュートン　　1686年。

ついでに、　この　ホームページは、代数曲線を主に紹介しているのでとりあげていない

　サイクロイド　cycloidは、エピサイクロイやハイポサイクロイドの仲間でそれら以上に

よく研究されています。上であげた、Brieskorn　他の本の同じ２６頁に　サイクロイドが

研究された時期および研究者が書かれています。

　　　　Jacob Bernoulli, Johann Bernoulli, Newton, Leibnitz,l'Hospitalらの研究、

　　　　Charles Bouvelles 1501年、

　　　　Nicolaus von Cues 1454年 ?、

　　　　Descartes デカルト　　1596-1650年、

　　　　Fermat フェルマー　 1601-1665年、

　　　　Galilei ガリレイ　　1590年

　　　　Mersenne 1615年、

　　　　Pascal パスカル　1623-1662年、

　　　　Roberval 1602-1675年、

　　　　Wallis ワリス　　1616-1703年、

　　　　Guido Grandi 1728年。　　

また、サイクロイドは、最速降下線　brachistochroneとしても有名です。　　

　ハイポロイドやサイクロイドをもう少し一般化して、実数 a, bと　整数 m, n

に対して、複素形で、　z(t) =a Exp[i m t] +b Exp[i n t],

　実形で、　　

　　　　x=a Cos[m t] +b Cos[ n t],

　　　　y=a Sin[m t] +b Sin[n t]

と媒介変数表示される曲線を考えてみましょう。ここでは、次のような場合を

　　考えてみることにします。

　第(III)章　　曲線　その３　 a=1, m=-k, b > 1, n=(k+1) [k=1,2,3, 4, ....]

すなわち　　

　　　　　x= Cos[ k t] +b Cos[ (k+1) t],

　　　　　y=- Sin[k t] +b Sin[ (k+1) t]

( 0 < t < 2 Pi) [k=1, 2, 3, 4, 5, .......]

より、幾何学的な観点で、ハイポロイドやサイクロイドを眺めると、これらは円C の上を

転がる別の円 C₁の周上の動点　P の軌跡です。　Pが、円　C₁ の周上の点でないと

き、P の軌跡を、　ハイポトロコイド　hypotrocoid ,エピトロコイド　epitrocoid

と言います。　そのような意味では、上記の曲線は、[k/(k+1)] [1/b]倍し、　

(k/(k+1)) (1/b) =g とすれば、　0 < g < k/(k+1) < 1が成り立ち、

　　x₁ = (k/(k+1)) Cos[ s ] + g Cos[ {(2k +1)/(k+1)-(k+1)/(k+1)} s] ,

　　y₁ = (k/(k+1)) Sin[ s ] -g Sin[ {(2k+1)/(k+1)-(k+1)/(k+1)} s]

　と媒介変数表示されるハイポトロコイドです。

　ここで、上記のような　g　の代わりに

　 k/(k+1) < g < 1　　に対応するハイポトロコイドを考えると、

　　0 < g < k/(k+1) の場合とはかなり違ったものができます。　

g=k/(k+1) のときは、正葉線となります。　

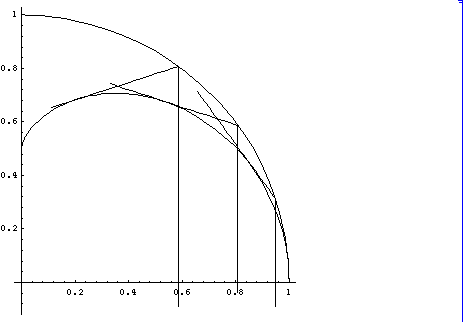
(1) k=1 の場合

　上の図は、　b = 1.8 の場合に対応するものです。bを大きくすると、曲線は、円周に近づ

きます。例えば、 b= 3.5 とすると、下の図のようになります。

　　　逆に、bを小さくして、1に近づけると、曲線における花びらの部分が、長細くなります。

例えば、b=1.2 とすると、下の図のようになります。

　　(2) k=2の場合　k=1 の場合と同様に、 bの値を変化させてそれに対応する曲線を眺めてみましょう。　

b= 1.2

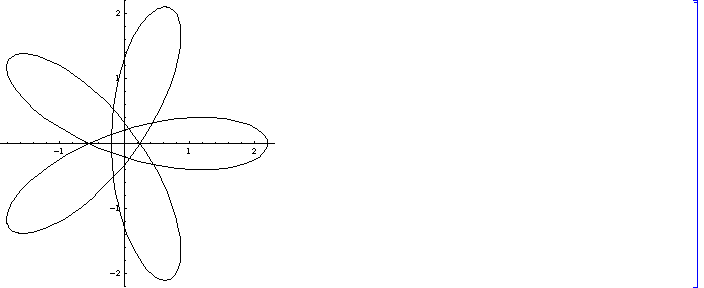
b=1.6

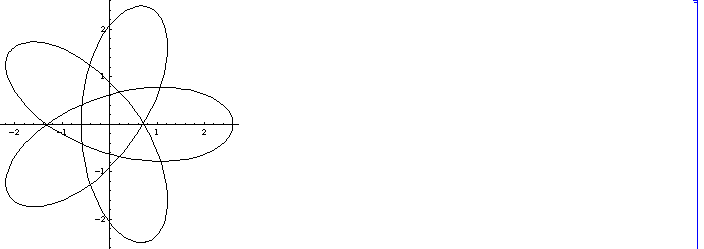
b=3.4

(1) k=1, (2)k=2で特に興味深いのは、曲線が自己交差する点がどのように分布するかです。上のk=1, k=2 の場合を見て、k=3 の場合がどうなるか見当がつきますか?

(3) k=3, b=1.8 の場合　

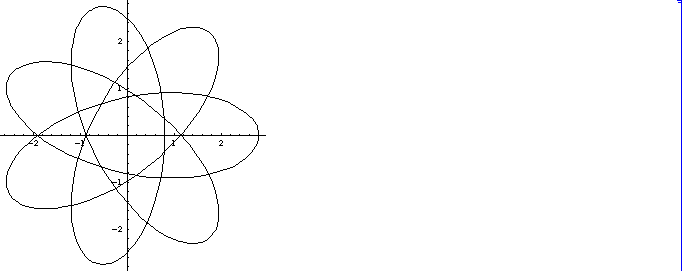
　第(IV)章　さて、(I), (II), (III) で登場した曲線は、いずれも x,y が、三角関数で媒介変

数表示されています。このような曲線で、別のタイプのものを考えてみましょう。　

Lissajou curve, リサジュ曲線

　　m, n を互いに素な自然数とし、

　　　　x= Sin[ m t], y=Sin[ n t]

( 0 < t < 2 Pi) により曲線を定めます。この曲線を、リサジュ曲線と言います。

さて、Sin[-m t]=-Sin[m t], Sin[-nt]=-Sin[n t]だからこの曲線は原点に関して対称です。

　リサジュ曲線という名前は、このような曲線をヨーロッパにおいて初めて研究した

　Lisssajouという人の名前から来ています。彼は、このよう曲線を、1850年に振動の

問題との関係で研究しました。前掲の Brieskorn ほかの本の65頁によれば、アメリカにお

いては、数学者で天文学者の Bowditchによって、1815年に　２重振り子　double

pendulumとの関係で、この曲線が研究されています。現在では、陰極線オシロスコープ

cathode ray oscilloscope でこれらの曲線を眺めることができます。

(i) m=1, n=2

この曲線　x=Sin[t], y=Sin[2 t] の媒介変数 t 　を消去すれば、

　　4 x⁴ -4 x² +y² = 0なる関係式が得られる。従って、

　　　y= 2 x Sqrt[1 -x²] , y= -2 x Sqrt[1-x²] ( -1 < x < 1)

なる２つの関数のグラフを合わせたものにも、この曲線はなっています。

(ii) m=2, n=3

　さて、　

Sin[ 2 t]=-Sin[Pi -2t]=-Sin[2 (Pi/2 -t)]

Cos[3 t]=Sin[Pi/2 -3t]= -Sin[3 Pi/2 -3t]=- Sin[3 (Pi/2 -t)]　

　　が成り立ちますから、この曲線を x=Sin[2 s], y=Cos[3 s] ( 0 <s < 2 Pi) と媒介変数表

示することもできます。

(iii) m=2, n=5

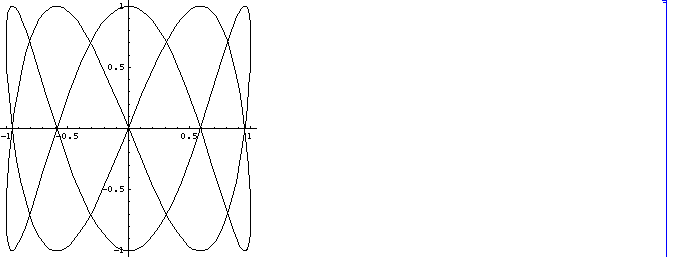
　　さて、

　　Sin[2 t]= Sin[Pi-2t] =Sin[2 (Pi/2 -t)]

　Cos[5 t] =Sin[Pi/2 -5 t] =Sin[5 Pi/2 -5t]=Sin[5 (Pi/2 -t)]

　ですから、この曲線を　x= Sin[2 s], y= Cos[5 s] ( 0 < s < 2Pi)

と媒介変数表示することもできます。

(iv) m=3, n=5

(v) m=4, n=5

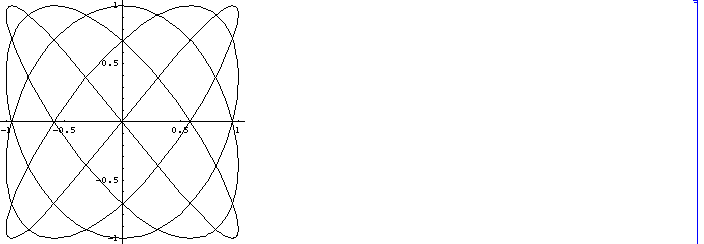
　　 Sin[-4(t+Pi)]=-Sin[4t], Sin[-5(t+Pi)]=Sin[Pi -5t]=Sin[5t]

ですから、この曲線は、y軸に関して対称です、さらに

　　　　Sin[4t]=-Sin[2Pi -4t]=- Sin[4 (Pi/2 -t)]

　　　Cos[5t]=Sin[Pi/2 -5t]=Sin[5 Pi/2 -5t]=Sin[5 (Pi/2-t)]　ですから

　この曲線をx=Sin[4 s], y=Cos[5 s] ( 0 < s < 2 Pi)と媒介変数表示することもできます。

(vi) m=5, n=7

　(vii) m=5, n=9

　　cf. (i) 永尾　汎　ほか　”数学 C”

　　　　（数研出版）pp. 88, pp.194

　　　(ii) 　藤田宏、前原昭二　編 ”数学 C”

　　　　　(東京書籍) pp. 84-85　

　　　(iii) 山本芳彦　編　”数学 C”　（啓林館）pp. 101-102, pp.206-207

　　リサジュ曲線は、x軸方向にも単振動し、y軸方向にも単振動する質点の軌跡です。この

　意味で、教科書 (i) , (ii) (数研出版, 東京書籍) のように

　　x= Sin[ m t], y= Sin [ n t] ( 0 < t < 2 Pi)

とする、のではなく教科書　 (iii) （啓林館）のように、

　　　x= Sin[ m t], y= Cos [ m t] ( 0 < t < 2 Pi )

を考え、これをリサジュ曲線と呼ぶこともあります。例えば、

(viii) x=Sin[3 t], y=Cos[5 t] ( 0 < t < 2 Pi)

(ix) x= Sin[5 t], y=Cos[7 t] ( 0 < t < 2 Pi)

(x) x=Sin[5 t],y=Cos[9 t] ( 0 < t < 2 Pi)

　となります。　　

さて、(IV) リサジュ曲線で紹介した曲線のうち、

(iv) x= Sin[3 t], y=Sin[5 t]

(vi) x=Sin[5 t], y=Sin[7 t]

(vii) x=Sin[5 t], y=Sin[7 t]

などは曲線が途中で途切れているとの印象を受けます。

例えば、(iv) について考えてみよう。

　　　Sin[3 t] = -4 (Sin[t])^3 +3 Sin[t],

Sin[5 t]= 16 (Sin[t])⁵ -20 (Sin[t])³ + 5Sin[t]

ですから、上で描いた曲線は、

　　　x= -4 s³+3 s, y= 16 s⁵ -20s³ +5 s (-1 < s < 1)

を描いたことになります。ここで、s を　-1 から　+1まで動かすという制約をとり払えば、

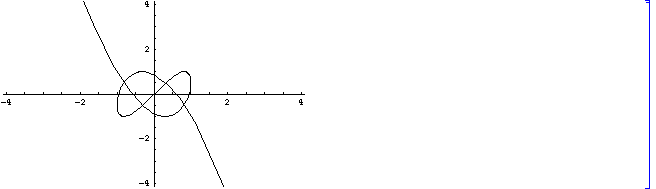
という（ような）曲線となります。この曲線は、長さが有限の辺をもつ長方形のなかにはおさまらないので、その部分をここでは描いています。　xと　y は、

　　　　16 x⁵ -20 x³ +5 x +4 y³-3 y = 0　

　という関係式を満たします。　

　第(V)章　これまで考えてきた曲線をもう少し一般化して、x, yがともに、Cos[t], Sin[t]

の有理関数で表わされ、 Tan[s]= y/x なる変数　s を用いて

r = Sqrt[ x² +y²] または　r²=x² +y² が、Cos[s], Sin[s]

　または、有理数　a > 0 に対する　Cos[a s], Sin[a s]の多項式としてあらわ

　されるものを考えましょう。

　　(i) まず、Lemniscate , レムニスケート, 連珠形

(ベルヌーイのレムニスケート、 lemniscate ofBernoulli )

　 x = Cos[t]/(1 +(Sin[t])² ),

　y= Sin[t] Cos[t]/(1 +(Sin[t])²)

( 0 < t < 2 Pi)

を眺めてみましょう。

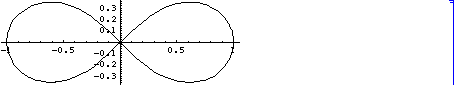
　( cf. リマソンについての教科書の記述、

　　　　永尾　汎　ほか　”数学 C”

　　　　（数研出版）pp. 92, 演習問題 17. )

　　　　上記のような媒介変数表示のとき、

　　　　　　　　　　y/x = Sin[t]

　　だから　　x =R Cos[s], y = R Sin[s]

とすれば、y²/x² = (Tan[s])²　であり、　

　　r²= x² +y² ={(Cos[t])² +(Sin[t])² (Cos[t])²}/{1+(Sin[t])²}²

=(Cos[t]) ²/{1 +(Sin[t])²} ={1-(Sin[t])²}/{1+(Sin[t])²}

={1 -y²/x²}/{1+y²/x²}={ 1 -(Tan[s])²}/{1+(Tan[s])²}

=2 (Cos[s])² -1 =Cos[2 s]　　となります。

　x, y は、次のような方程式を満たします

　　　(x² +y²)² -(x²-y²) = 0

この方程式を　”同次化”　しますと、

　　　X⁴ +2 X² Y² +Y⁴- X² Z² + Y² Z² =0

という方程式が得られます。この曲線を”複素射影代数曲線”として扱うと、

　(x, y)=(0, 0) 　即ち　(X, Y, Z)=(0, 0, 1)なる点　と　無限遠点でしかも虚の点

　　(X, Y, Z)= (1, i, 0) および (X, Y, Z)=(1, -i, 0) の３点で　通常２重点を持ちます。

　また、　この曲線は、リサジュ曲線を扱ったときに登場した

　x= Sin [t], y= Sin[2 t] ( 0 < t < 2 Pi )

という曲線と見かけの上でかなり似ています。こちらの方は方程式

　　　　 4 x⁴ -4 x² + y² =0

　　をみたし、さらにこれを　”同次化”　すると、

4 X⁴- 4 X² Z² +Y²Z² = 0

を満たします。この曲線を、”複素射影代数曲線”として扱うと、

　　(x, y)=(0,0) 　即ち　(X, Y, Z)=(0,0,1)　で　通常２重点をもち、

　　(X, Y, Z)= (0, 1, 0)なる無限遠点で接触結節点を持ちます。　この点の近くでの

　曲線の状況を見ましょう。　Y=1, X=x, Z=i z と置き非同次の方程式

　　　　4 x⁴ + 4 x² z² -z² =0

を考えます。このとき、 z = 2 x² / Sqrt[1 -4x²], z=- 2 x²/Sqrt[1 - 4 x²]

が得られます。これを描くと次のようになります。

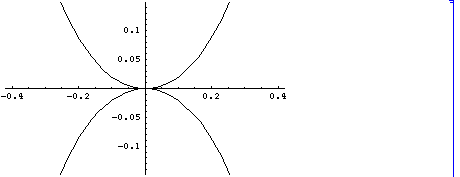
これらの考察で、レムニスケートと　リサジュの m=1, n=2の場合が本質的に異なる性質をもつことがわかる。m=1, n=2のリサジュの方は、　８の字曲線　the figure 8 curve

とか、Geromoのレムニスケート　the lemniscate of Geromo という名前が

付いています。(cf. A. Gray " Modern Differential Geometry ofCurves and Surface ",

CRC Press, pages 21-22). 　

　　”複素射影代数曲線”　とみて、４次の既約代数曲線で、１個の通常２重点と１個の接触

結節点を持ち、しかも有理曲線であるという性質を、次の４次曲線も持ちます。次の曲線はそう

いう意味では８の字曲線の仲間です。

　　(x² +y² -3 x)² -4x² (2 -x)

　　　= x² -2 x³ +x⁴ -6 xy² +2 x² y² +y⁴ = 0　　

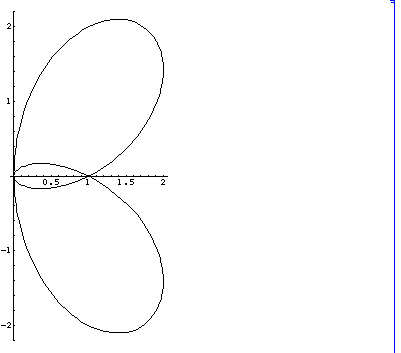
　この曲線は、次のように媒介変数表示できます。

　　　 x = 2 (Sin[t])² = 1 - Cos[2 t] ,

　　　y= Sqrt[2] Sin[t] + Sin[2 t]

　　( 0 < t < 2 Pi).

　(ii) 次にパスカルのリマソン Limacon 　

　　　　x=(2 Cos[t] +1) Cos[t],

　　　　y=( 2 Cos[t] +1) Sin[t]

　　　　　　　　　( 0 < t < 2 Pi)

　　を眺めてみましょう。

　この曲線は、

　　　(x² +y² -2 x)²-(x² +y²)

=3 x² -4 x³ +x⁴ -y² -4x y² +2 x² y² +y⁴ =0

という方程式を満たす。　r = 2 Cos[t] +1.

　”複素射影代数曲線”としてこの曲線をみて、同次方程式

　　　(X² +Y² -2 X Z)²-X² Z² -Y² Z² = 0

を考える。リマソンは、　(x, y)=(0, 0) 即ち　(X, Y, Z)=(0, 0, 1)に通常２重点を持ちま

す。また、虚の無限遠点　(X, Y, Z)=(1, i, 0) および、(X, Y, Z)=(1,-i, 0) において単純尖

点を持ちます。さらに、上で考えた曲線を一般化して、1　より大きい bに対

し、　　r =b Cos[t] +1 即ち

　　x =(b Cos[t] +1) Cos[t], 　y= (b Cos[t] +1) Sin[t]

　　　( 0 < t < 2 Pi) とすれば、この曲線は、方程式

　　　x⁴+2 x² y² +y⁴+(b² -1) x² -2 b x³ -y²-2 b x y²

　　　　　= (x² +y² -b x)²-(x² +y²) = 0

を満たし、”複素射影代数曲線”　(X² +Y² -b XZ) -(X² +Y²) Z² =0 は、

　(X, Y, Z)=(0, 0, 1) で通常２重点を、 (X, Y, Z)=(1, i, 0) および(X, Y, Z)=(1, -i, 0)

で、単純尖点を持ちます。b=2の場合に、この単純尖点を見てみましょう。

　X=1, Z =z, Y=i y として、z 軸を横軸、 y軸を縦軸にとって曲線

　　　y⁴ +y² z² +4 y²z -2 y² +3 z²-4 z +1 = 0 　　

　を描きますと、次のようになります。

　　　代数曲線論の立場からは、リマソンは、その双対曲線がリマソンと（射影的に）同形で

　あるという性質が注目されます。

　　(ii) ”数学 C”でよく取り上げられる曲線の別の例として、正葉曲線、バラ曲線

　　　　 x = Sin[ a t] Cos[t] =(1/2) ( Sin[ (a +1) t] +Sin[ (a-1)t])

　　　　y= Sin[a t] Sin[t] = (1/2) (- Cos[(a+1) t] +Cos[ (a-1) t])

　　があります。ここで、 a > 0 は、正　の有理数とします。　　

　　a=3 の場合は、次のような曲線となります。

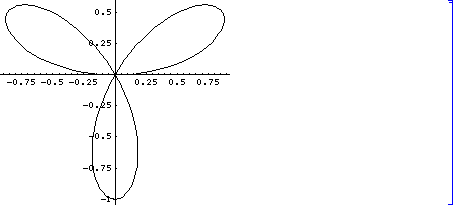
　　　この曲線は、

　　　　　　　(x² +y²)² +y (y² -3 x²) = 0

　　　　という方程式を満たします。

　第 (VI) 章　補論　　射影幾何学の古典的定理の紹介

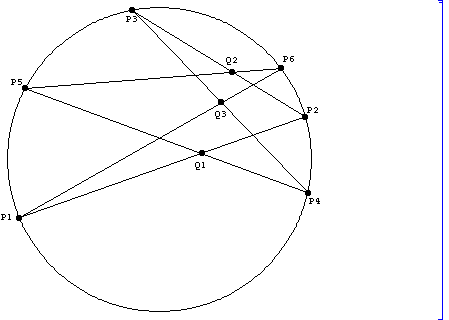
　（１）Pascal の定理　既約な２次曲線 C に内接する６角形の

　　　　３組の対辺の交点は、一直線上にある。　

　註　　例えば既約な２次曲線として楕円を考える場合、楕円上にある６点　

　　P₁, P₂, P₃, P₄,P₅, P₆が時計回りまたは反時計回りに配置されている

　場合だけでなく、別　の並びをしていてもこの定理は成立します。

　この定理を使った例題を一つ提示します。　

　　例題　　単位円周上 x²+y² =1 上に６点を次のように取る。

　P₁= (-12/13,-5/13), P₂= (24/25, 7/25),

　P₃=(-11/61, 60/61),P₄= (40/41, -9/41),

　P₅=(-15/17, 8/17),P₆= (4/5, 3/5).

　ここで、P₁,P₂ を結ぶ直線 L₁とP₄, P₅を

　結ぶ直線 L₂の交点をQ₁とする。

　P₂,P₃を結ぶ直線 L₃とP₅, P₆を結ぶ直線L₄

　の交点をQ₂とする。

　P₃,P₄を結ぶ直線 L₅とP₆,P₁を結ぶ直線L₆

　の交点をQ₃とする。

　　　1) Q₁= (120/431,17/431),

　　　Q₂= (51/106,61/106),

　　Q₃= (32/79,207/553),

　　　となることを示せ。

　　　2) 3点 Q₁,Q₂, Q₃が同一直線上にあること

　　を示せ。

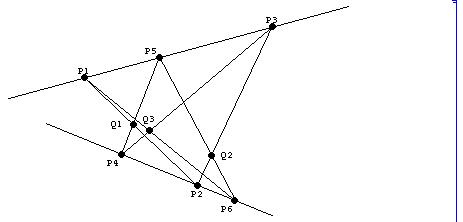
(2) Pappusの定理 Pascalの定理における"既約な２次曲線" C を、二つの

　異なる２直線の和に置き換えた定理　

　　この定理を使った例題を一つ提示します。　

　例題　3点　P₁=(1, 5),P₃=(6, 15), P₅=(3, 9) は、直線L : y=2 x +3 上にある。

　　また、３点 P₂=(4,-16),P₄=(2,-10), P₆=(5,-19)は、

　　直線 M : y=-3 x -4 上にある。

　　ここで、２点　P₁,P₂を結ぶ直線 L₁と　２点 P₄,P₅ を

　　結ぶ直線L₂の交点をQ₁とする。

　　　２点　P₂,P₃ を結ぶ直線 L₃ と　２点P₅, P₆を

　　結ぶ直線L₄の交点をQ₂とする。

　　　２点　P₃,P₄ を結ぶ直線 L₅ と　２点P₁, P₆ を

　　結ぶ直線L₆の交点をQ₃とする。

　　1) Q₁=(30/13, -54/13),Q₂=(258/59, -603/59),

　　　Q₃=(134/49,-265/49)

　　となることを示せ。

　　2) 3点 Q₁,Q₂, Q₃が同一直線

　　　　y=-(47/16) x　+(21/8)上にあることを示せ。　　

　　　　　　　　　　　　　　　　END