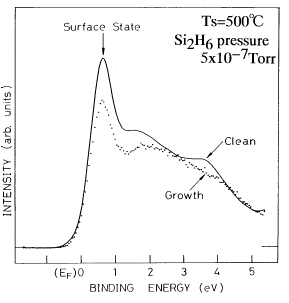
恾侾丂Si(100)2x1惔忩昞柺乮幚慄乯偲偙傟傪婎斅偲偟偨僕僔儔儞GS-MBE拞乮揰乯偺UPS僗儁僋僩儖丅
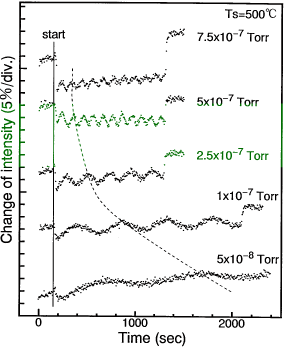
恾俀丂僕僔儔儞GS-MBE拞偵尒傜傟傞UPS怳摦丅僕僔儔儞偼start偱帵偟偨幚慄偐傜摫擖偟偰偄傞丅
 恾侾丂Si(100)2x1惔忩昞柺乮幚慄乯偲偙傟傪婎斅偲偟偨僕僔儔儞GS-MBE拞乮揰乯偺UPS僗儁僋僩儖丅 |
 恾俀丂僕僔儔儞GS-MBE拞偵尒傜傟傞UPS怳摦丅僕僔儔儞偼start偱帵偟偨幚慄偐傜摫擖偟偰偄傞丅 |
俀丏丂倀俹俽怳摦偺婲尮
丂倀俹俽怳摦偺婲尮偺壜擻惈偲偟偰埲壓偺俁偮偑峫偊傜傟傞丅
嘆Si偺扨尨巕憌惉挿偵偲傕側偆昞柺峳偝偺廃婜揑曄壔丅
嘇Si昞柺忋偺僟儞僌儕儞僌儃儞僪偲寢崌偟偨悈慺検偺廃婜揑曄壔丅
嘊Si偺扨尨巕憌惉挿偵偲傕側偆昞柺嵞攝楍峔憿偺廃婜揑曄壔丅
丂嘆偼傛偔抦傜傟偰偄傞RHEED嫮搙怳摦偺婲尮偱傕偁傞丅嘇偼嘆偺昞柺峳偝偺曄壔偵偲傕側偭偰
惗偢傞壜擻惈偑偁傞丅嘊偼
俀亅侾丂幚尡曽朄
幚尡偼崅僄僱儖僊乕壛懍婍尋媶婡峔曻幩岝幚尡巤愝BL-11D偱峴偄丄梡偄偨憰抲偼変乆偑奐敪偟偨
偦偺応倀俹俽僔僗僥儉偱偁傞丅
曻幩岝偺僄僱儖僊乕偼23.3eV偱擖幩妏偼45亱丄倀俹俽怳摦應掕拞偺岝揹巕庢傝弌偟
妏偼傎傏昞柺悅捈偱偁傞丅偨偩偟丄屻偵暘偐傞傛偆偵庢傝弌偟妏偼尩枾偵悅捈偱偼側偔
丄偙偺妏搙偑倀俹俽怳摦傪敪尰偝偣傞忋偱廳梫側梫慺偱偁傞丅Si(100) 0.2亱off僂僃僴
乕傪3x25x0.35mm偵愗傝弌偟惉挿婎斅偲偟偨丅偙偺婎斅傪壔妛慜張棟傪峴偭偨屻丄恀嬻拞
偱1000亷偺捠揹壛擬偡傞偙偲偵傛傝惔忩昞柺傪摼偨丅Si(100)昞柺偼捠忢僟僽儖僪儊僀儞
偺2x1嵞攝楍乮懄偪2x1+1x2乯傪偲傞偑丄揔摉側張棟偵傛傝僔儞僌儖僪儊僀儞壔偑壜擻偱偁
傞丅屻偱弎傋傞傛偆偵昞柺偺僔儞僌儖僪儊僀儞壔偑倀俹俽怳摦偺婲尮傪扵傞忋偱廳梫偲側偭
偨丅杮幚尡偱偼1000亷偺挿帪娫捠揹壛擬傾僯乕儖偵傛偭偰僔儞僌儖僪儊僀儞壔偟丄偦偺捈棳
揹棳偺岦偒傪昞柺僗僥僢僾偵懳偟up-down偵偡傞偐丄down-up偵偡傞偐偱昞柺傪2x1偵偡傞偐1x2偵
偡傞偐傪寛掕偡傞偙偲偑偱偒偨丅惉挿偵梡偄偨僕僔儔儞僈僗偺弮搙偼99.99亾偱偁傞丅幚尡曽朄偺奣棯恾傪恾俁偵
帵偡丅
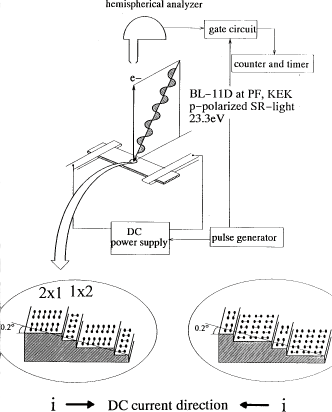 恾俁丂幚尡憰抲偺奣棯恾偲僔儞僌儖僪儊僀儞昞柺偺捠揹揹棳曽岦埶懚惈 |
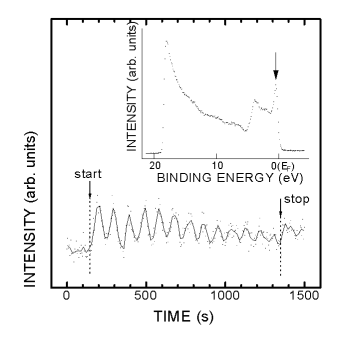 恾係丂屌懱僜乕僗MBE拞偵尒傜傟傞UPS怳摦丅憓擖恾偼惔忩昞柺偺UPS僗儁僋僩儖偱丄UPS怳摦偱娤應偟偨 弨埵傪栴報偱帵偟偰偄傞丅 |
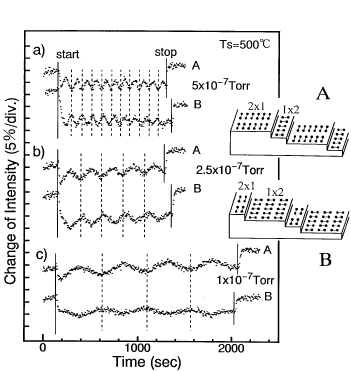 恾俆丂僕僔儔儞GS-MBE拞偺UPS怳摦丅惉挿奐巒昞柺偑2x1偺応崌(A)偲1x2偺応崌(B)偱埵憡偑斀揮偟偰偄傞偺偑暘偐傞丅 |
偙偺寢壥偼丄倀俹俽怳摦偺尨場偑僔儕僐 儞扨尨巕憌惉挿偵傛傞昞柺嵞攝楍峔憿丆2x1偲1x2丆偺廃婜揑側擖傟戙傢傝偵傛傞傕偺偱偁傞偙偲 傪帵偟偰偄傞丅偡側傢偪丄埲壓偺傛偆側儌僨儖偱偁傞丅Si(100)昞柺偼偦偺寢徎峔憿偐傜2x1昞柺忋 偵侾尨巕憌寢徎偑惉挿偡傞偲昁慠揑偵1x2昞柺偵側傞丅媡偵1x2昞柺忋偵侾尨巕憌惉挿偡傞偲2x1昞柺 偵側傞丅偦偙偱1x2昞柺偵斾傋2x1昞柺偺岝揹巕嫮搙偑庛偄偲偡傞丅偡傞偲2x1昞柺傪惉挿奐巒昞柺偲 偡傞倀俹俽怳摦偼恾俇嵍偺傛偆偵嫮搙憹壛偱巒傑傝丄1x2昞柺傪惉挿奐巒昞柺偲偡傞倀俹俽怳摦偼恾 俇塃偺傛偆偵嫮搙尭彮偱巒傑傞丅偦偟偰偳偪傜傕俀尨巕憌惉挿傪侾廃婜偲偡傞怳摦偑惗偢傞丅幚嵺偵 偼慜偵弎傋偨傛偆偵悈慺偵傛傞嫮搙尭彮暘偑偁傞偑丄偙傟偼抁帪娫偱朞榓偡傞偺偱堦掕偺嫮搙偑惉挿 拞偺傒嵎偟堷偐傟偨傛偆側嫮搙曄壔偵側傞丅
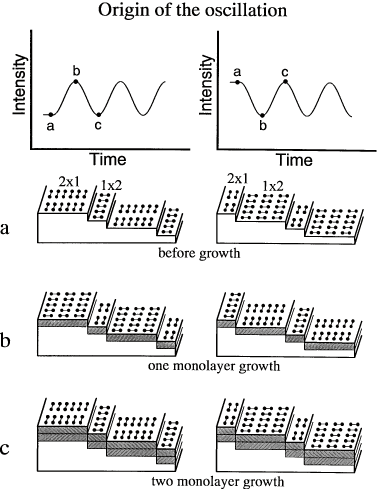 恾俇丂UPS怳摦偺敪尰婡峔儌僨儖 |
俁丏丂2x1丄1x2昞柺偺倀俹俽嫮搙嵎偺尨場
丂忋偺儌僨儖偺拞偱2x1偲1x2昞柺偺倀俹俽嫮搙偺堘偄偼側偤惗偠傞偺偐偲偄偆媈栤偑巆傞丅偙傟傪柧傜偐
偵偡傞偨傔2x1,1x2椉惔忩昞柺偺倀俹俽僗儁僋僩儖嫮搙傪曃岝埶懚惈丄妏搙埶懚惈偺娤揰偐傜徻嵶偵挷傋偨丅
俁亅侾丂幚尡曽朄
丂幚尡偼俀丏偲摨條偵BL-11D偱峴偄丄梡偄偨憰抲偼PF晅懏偺ARPES憰抲偱偁傞丅椼婲岝偼23.3eV偺捈慄曃
岝偟偨曻幩岝偱擖幩妏偼45亱偱偁傞丅Si(100)帋椏偼[110]曽岦偵3'丄[1-10]曽岦偵30''埲撪偱僼儔僢僩
偺柺惛搙傪帩偭偰偄傞丅帋椏僒僀僘丄昞柺慜張棟朄偼俀丏偲摨條偱偁傞丅恀嬻拞偱1000亷偺捠揹壛擬偡
傞偙偲偵傛傝惔忩昞柺傪摼偨丅偦偺屻昞柺偺嵞攝楍傪僔儞僌儖僪儊僀儞壔偡傞偨傔偵悢昐侌偺
Si buffer layer偲1000亷偺傾僯乕儖傪悢夞孞傝曉偟偨丅LEED偺夞愜僗億僢僩偺嫮搙傪應掕偟丄偦偺
寢壥major domain:minor domain=4:1偺嵞攝楍昞柺傪摼偨丅major domain偼俀丏偱弎傋偨傛偆偵帋椏偵
棳偡捈棳揹棳偺岦偒傪斀揮偝偣1000亷傾僯乕儖偡傞偙偲偵傛傝曄偊傞偙偲偑偱偒傞丅偙偙偱偼Si僟僀儅乕
楍偑椼婲岝偲専弌偟偨岝揹巕偑嶌傞柺偵懳偟悅捈偱偁傞傛偆側椞堟偑major domain偱偁傞応崌2x1昞柺偲
屇傃丄Si僟僀儅乕楍偑柺撪偵偁傞傛偆側椞堟偑minor domain偱偁傞応崌1x2昞柺偲屇傇偙偲偵偡傞丅帋椏
偺曽埵妏傪夞揮偝偣傞偙偲偵傛傝2x1昞柺偵偟偨傝1x2昞柺偵偡傞偙偲偑偱偒傞偑丄曽埵妏傪曄偊偢偵忋偱
弎傋偨捠揹曽岦傪曄偊偰傾僯乕儖偡傞偙偲偵傛傝2x1偲1x2傪曄偊傞偙偲傕偱偒傞丅杮尋媶偱偼椉曽朄偺応崌
偲傕應掕傪峴偭偨丅
俁亅俀丂幚尡寢壥
丂恾俈偼捠揹曽岦傪曄偊傞偙偲偵傛偭偰嶌惉偟偨Si(100)2x1乮攋慄乯偲1x2乮幚慄乯惔忩昞柺偺妏搙暘夝岝揹
巕暘岝乮ARUPS乯僗儁僋僩儖偱偁傞丅岝揹巕偺庢傝弌偟妏偑兤亖侽亱偱椉僗儁僋僩儖偼姰慡偵堦抳偟偰偄傞丅
偡側傢偪normal emission偱偺曃岝埶懚惈偵傛傞嫮搙嵎偼柍偄偙偲偑暘偐傞丅兤亜侽亱偱偼寢崌僄僱儖僊乕偑
0.5eV乣2eV偲3.5eV乣4.5eV偺斖埻偱嵎堎偑惗偠偰偄傞丅偙偺嵎堎偼曃岝埶懚惈偲偄偆傛傝偼昞柺弨埵偺妏搙暘
嶶惈偵傛傞傕偺偲峫偊傜傟傞丅
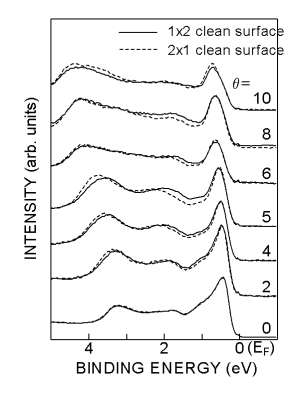 恾俈丂Si(100)2x1(攋慄乯偲1x2乮幚慄乯惔忩昞柺偺ARUPS僗儁僋僩儖丅兤偼岝揹巕偺庢傝弌偟妏丅 |
丂偙傟傑偱倀俹俽怳摦偼normal emission偱尰傟傞偲峫偊偰偄偨丅偟偐偟尩枾側妏搙暘夝應掕偱偼normal偱2x1
偲1x2偺倀俹俽嫮搙偵嵎偼側偔丄normal偐傜傢偢偐偵曄偊傟偽椉僗儁僋僩儖偵嵎偼尰傟傞帠偑暘偐偭偨丅傕
偟倀俹俽怳摦偺敪尰忦審偑尩枾偵偼normal emission偱偼側偔丄偦偟偰恾俈偵帵偟偨傛偆側昞柺弨埵偺妏搙
埶懚惈傪婲尮偲偡傞側傜偽丄2x1偲1x2偺嵎暘僗儁僋僩儖偑倀俹俽怳摦偺怳暆偺寢崌僄僱儖僊乕埶懚惈偵堦抳
偡傞偼偢偱偁傞丅偦偙偱峀斖埻偵傢偨傞岝揹巕僄僱儖僊乕偱倀俹俽怳摦傪應掕偟偨乮恾俉乯丅怳摦偼偙傟傑
偱弎傋偰偒偨昞柺弨埵埵抲偩偗偱偼側偔丄峀斖埻偵傢偨傝敪尰偟偰偄傞偺偑傢偐傞丅偟偐傕b乣d偺娫偱傒傜
傟傞怳摦偼丄g乣l偺娫偱傒傜傟傞怳摦偵懳偟埵憡偑斀揮偟偰偄傞丅怳暆偺曄壔偲嵎暘僗儁僋僩儖傪斾妑偟偨
寢壥丄兤亖俆亱偺嵎暘僗儁僋僩儖偑嵟傕傛偔怳暆偺曄壔偲堦抳偡傞偙偲偑傢偐偭偨乮恾俋乯丅
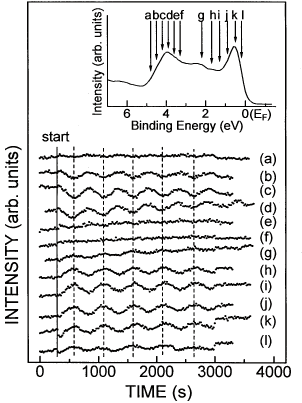 恾俉丂僕僔儔儞GS-MBE拞偺UPS怳摦丅條乆側岝揹巕僄僱儖僊乕(a-l乯偱應掕偟偰偄傞丅 |
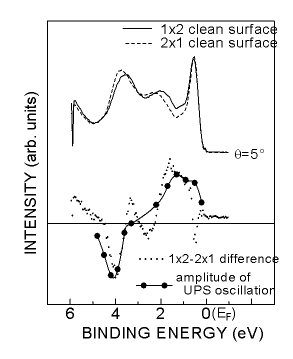 恾俋丂兤亖俆亱偺ARUPS僗儁僋僩儖偺2x1偲1x2偺嵎暘乮揰乯偲UPS怳摦偺怳暆偺曄壔乮崟娵偍傛傃幚慄乯偲偺斾妑丅 |
丂俁亅侾偱弎傋偨傛偆偵曽埵妏傪曄偊傞偙偲偵傛偭偰傕2x1偲1x2昞柺偺嵎暘僗儁僋僩儖傪摼傞偙偲偑偱偒傞丅偙
偺応崌偺寢壥偼恾俈偲傎傏堦抳偟偨丅
丂埲忋傛傝丄偙傟傑偱娤應偟偨倀俹俽怳摦偼兤亖俆亱偱應掕偟偨傕偺偱偁傝丄2x1偲1x2偺倀俹俽僗儁僋僩儖偺嫮
搙嵎偼椉昞柺偱偺妏搙埶懚惈偺堘偄偵傛傞傕偺偱偁傞偙偲偑柧傜偐偲側偭偨丅
係丏丂俼俫俤俤俢怳摦偵傛傞倀俹俽怳摦廃婜偺摨掕
偙傟傑偱偺寢壥偵傛傝倀俹俽怳摦偺婲尮偼柧傜偐偲側偭偨偑丄忋偺儌僨儖傪妋棫偡傞偨傔摨惉挿忦審偱
俼俫俤俤俢怳摦應掕傪峴偄倀俹俽怳摦偺廃婜偑偳偺偔傜偄偺惉挿偵懳墳偡傞偺偐傪挷傋偨丅嬶懱揑偵偼僔
儞僌儖僪儊僀儞Si(100)忋偺Si2H6傪梡偄偨僈僗僜乕僗暘巕慄僄僺僞僉僔拞偵俼俫俤俤俢夞愜僗億僢僩嫮搙傪
娤應偟偨丅Laue1/2師夞愜僗億僢僩偼惉挿帪娫偲偲傕偵廃婜怳摦偟偨丅偙傟偼昞柺嵞攝楍峔憿偺岎戙偑侾俵俴
偺惉挿枅偵惗偢傞偐傜偱偁傞丅偡側傢偪怳摦偺侾廃婜偼僔儕僐儞俀尨巕憌偺惉挿偵懳墳偟丄偙傟偵傛傝僔儕
僐儞偺惉挿懍搙偑傢偐傞丅條乆側GSMBE忦審偱惉挿懍搙傪應掕偟丄倀俹俽怳摦朄偱摼傜傟偨廃婜偑偳偺偔傜偄
偺惉挿偵懳墳偡傞偐傪挷傋偨丅恾侾侽偼惉挿壏搙500亷偱丄僈僗埑傪墶幉偵偲偭偨偲偒偺倀俹俽怳摦偲俼俫俤俤
俢怳摦偺廃婜傪僾儘僢僩偟偨丅偡傋偰偺僈僗埑偱椉怳摦廃婜偼傎傏堦抳偟偰偍傝丄倀俹俽怳摦偺侾廃婜偼俀
尨巕憌偺惉挿偵懳墳偡傞偙偲偑宯摑揑偵帵偝傟偨丅偙傟偵傛傝倀俹俽怳摦偺婲尮偼昞柺嵞攝楍峔憿偺岎戙偵傛
傞傕偺偱偁傞偙偲偑捈愙揑偵帵偝傟偨丅
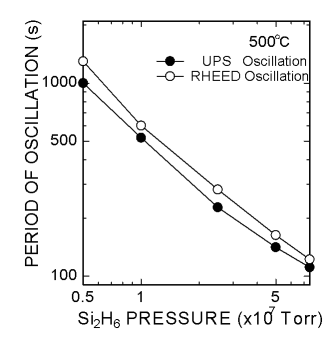 恾侾侽丂UPS怳摦廃婜偲RHEED怳摦廃婜偺斾妑丅 |
俆丏丂儌儞僥僇儖儘僔儈儏儗乕僔儑儞偵傛傞倀俹俽怳摦偺嵞尰
丂俀丏偍傛傃俁丏偱傢偐偭偨傛偆偵倀俹俽怳摦偺婲尮偼扨尨巕憌惉挿偵傛傞Si(100)昞柺偺2x1偲1x2偺
擖傟戙傢傝偵偁傞丅偟偐偟幚嵺偺寢徎惉挿偱惗偠傞昞柺斀墳偼丄昞柺尨巕偺儅僀僌儗乕僔儑儞岠壥丄
俀師尦妀惉挿丄僗僥僢僾僼儘乕惉挿側偳懡嵤偱偁傝丄恾俇偺儌僨儖偺傛偆側2x1偲1x2偑棟憐揑偵擖
傟戙傢傞憌忬惉挿偑婲偙傝摼傞偐偼柧妋偱側偄丅偦偙偱偳偺傛偆側惉挿慺夁掱傗惉挿忦審偑偁傟偽忋
偱帵偟偨婲尮偵婎偯偒UPS怳摦偑壜擻側偺偐傪専徹偡傞偨傔丄儌儞僥僇儖儘朄偵傛傞悢抣僔儈儏儗乕僔
儑儞偵傛傝倀俹俽怳摦偺嵞尰傪帋傒偨丅
丂惉挿儌僨儖傪埲壓偵帵偡乮恾侾侾嶲徠乯丅
嘆丂100x100偺僙儖傪梡堄偟丄2x1偲1x2偺僪儊僀儞斾棪偑4:1偵側傞傛偆偵偦傟偧傟偺僙儖偵尨巕傪愊傒忋偘傞丅
嘇丂偙偺僙儖偺忋偵儔儞僟儉偵尨巕傪棊偲偡丅
嘊丂偡傋偰偺僙儖偺嵟忋憌尨巕偵懳偟嵟嬤愙偺僙儖傊偺奼嶶傪峴偆丅偨偩偟偳偺嵟嬤愙僙儖偵堏傞偐偼
儔儞僟儉偱丄傑偨嵟嬤愙僙儖偺忬懺偵傛傝奼嶶偱偒傞妋棫俹偼丄丂丂
丂丂丂丂丂丂丂丂丂丂 丂丂
偲偡傞丅偙偙偱A偼掕悢丄n偼嵟嬤愙僙儖偺偆偪崅偝偑帺暘帺恎傛傝崅偄偐摨偠偱偁傞悢乮侽乣係乯丄
kT偼婎斅壏搙偵懳墳偡傞曄悢偱偁傞丅
嘋丂2x1偺僙儖悢傪僇僂儞僩偡傞丅偙偺悢偑倀俹俽嫮搙偵懳墳偡傞丅
嘍丂嘇偵栠傝昁梫側惉挿検傑偱偙傟傪孞傝曉偡丅
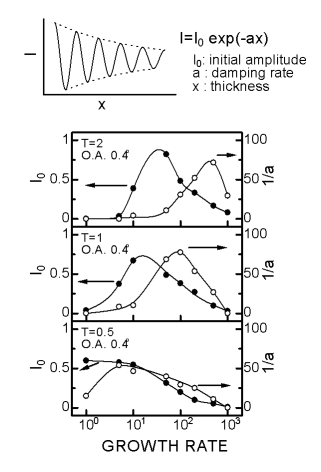
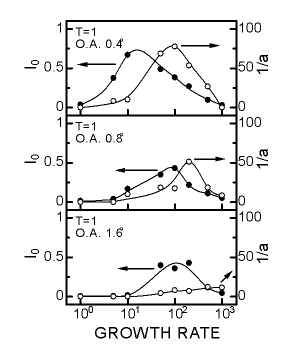
恾侾俀偼kT亖侾丄off-angle亖0.4亱偺寢壥偱偁傞丅恾拞rate偲偼嘇偱棊偲偡尨巕偺悢偱偁傝丄惉挿懍搙
偵懳墳偡傞丅堦尒偟偰暘偐傞傛偆偵怳摦尰徾偑柧妋偵尰傟偰偄傞丅rate偑50乣200偱偼30ML埲忋傕怳摦
偑帩懕偟偰偄傞偺偑暘偐傞丅
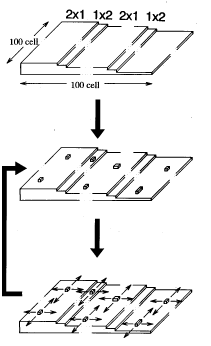 恾侾侾丂儌儞僥僇儖儘朄偵傛傞UPS怳摦僔儈儏儗乕僔儑儞偺僼儘乕僠儍乕僩丅 |
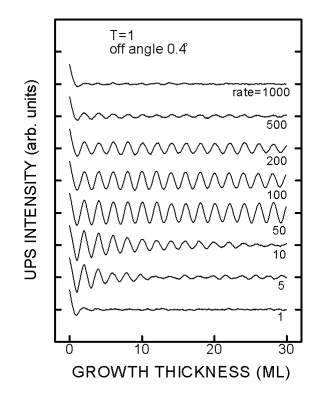 恾侾俀丂UPS怳摦偺僔儈儏儗乕僔儑儞寢壥丅 |
婎斅壏搙kT傪曄偊丄怳摦偺曪棈慄傪恾侾俁偺憓擖恾偱帵偟偨傛偆偵僼傿僢 僥傿儞僌偟偰丄摼傜傟偨僷儔儊乕僞傪傑偲傔偨丅惉挿懍搙偵懳偡傞尭悐棪a偺曄壔偐傜怳摦偼摿掕偺惉挿 懍搙偱挿帪娫帩懕偡傞偙偲偑暘偐傞丅偙傟偼師偺傛偆側棟桼偵傛傞傕偺偲峫偊傜傟傞丅惉挿懍搙偑戝偒偡 偓傞偲奼嶶偣偢偵懡偔偺尨巕偑棊偪偰偔傞偺偱憌忬惉挿偣偢俁師尦惉挿偟偰偟傑偄怳摦偼尭悐偡傞丅媡偵 惉挿懍搙偑彫偝偡偓傞偲奼嶶偑戝偒偔僗僥僢僾僼儘乕惉挿偟偰偟傑偄恾俇偺傛偆側2x1偲1x2偺擖傟戙傢傝 偑婲偙傜側偔側偭偰偟傑偆丅尭悐棪偺僺乕僋埵抲偼婎斅偑崅壏偵側傞偮傟偰惉挿懍搙偑戝偒偄傎偆偵僔僼 僩偟偰偄傞偑丄偙偺偙偲偼崱弎傋偨棟桼偲柕弬偟側偄丅惉挿婎斅偺off-angle傪曄偊偨寢壥傕摨條偱丄怳摦 尭悐棪偺僺乕僋埵抲偼off-angle偑戝偒偔側傞偵偮傟偰惉挿懍搙偺戝偒偄傎偆偵僔僼僩偟丄傑偨尭悐傕戝偒 偄乮恾侾係乯丅埲忋偺傛偆偵丄倀俹俽怳摦偼娙扨側奼嶶儌僨儖傪峫偊傟偽嵞尰偱偒丄傑偨揔摉側惉挿忦審傪 枮偨偣偽30ML埲忋偵媦傃帩懕偝偣傞偙偲偑偱偒傞丅
 恾侾俁丂UPS怳摦偺尭悐棪偲弶婜怳暆偺惉挿懍搙埶懚惈丅惉挿壏搙傪偄偔偮偐曄偊偰偄傞丅 |
 恾侾係丂UPS怳摦偺尭悐棪偲弶婜怳暆偺惉挿懍搙埶懚惈丅婎斅僆僼妏搙傪偄偔偮偐曄偊偰偄傞丅 |
俇丏丂傑偲傔
丂埲忋傪傑偲傔傞偲丄UPS怳摦偺敪尰偵昁梫側忦審偼嘆俀師尦妀傪偲傕側偆憌忬惉挿丄
嘇俀偮埲忋偺堎側傞揹巕忬懺傪帩偮昞柺偺弌尰丄偱偁傞丅偟偨偑偭偰偙偺忦審傪枮偨偣偽Si(100)忋
偺惉挿偵尷傜偢懠偺昞柺偱偺惉挿偵懳偟偰傕倀俹俽怳摦偑敪尰偡傞偲峫偊傜傟傞丅倀俹俽怳摦偲椶帡
偺尰徾偲偟偰俼俫俤俤俢怳摦偑抦傜傟偰偄傞偑丄僾儘乕僽偲偟偰崅懍偺揹巕慄傪梡偄傞偺偱寢徎惉挿
偵懳偡傞揹巕慄徠幩偺塭嬁偑柍帇偱偒偢丄揹巕慄徠幩偺桳柍偵傛傞惉挿懍搙傗惉挿枌幙偺堘偄偑寽擮偝
傟傞丅倀俹俽怳摦偼偙偺揰偵偍偄偰偦傟傎偳惉挿偵塭嬁傪梌偊側偄偲峫偊傜傟丄偁傝偺傑傑偺惉挿傪娤
應偱偒傞丅偟偐偟倀俹俽怳摦偼椼婲尮偺嫮搙丄専弌岠棪丄椼婲妋棪摍偺堘偄偵傛傝丄俼俫俤俤俢怳摦偵
斾傋偦偺嫮搙偑庛偔丄惉挿懍搙偑戝偒側応崌偱偼廫暘側S/N傪帩偮怳摦偑摼傜傟擄偄丅偟偨偑偭偰倀俹
俽怳摦偺墳梡柺傪峫偊傞忋偱偦偺戝嫮搙壔偼寚偐偣側偄丅偙偺偨傔偵偼埲壓偺傛偆側夵椙偑嫇偘傜傟傞丅
嘆丂椼婲岝偺崅婸搙壔丅偙偺偨傔偵偼崅婸搙曻幩岝側偳偺戝婯柾側巤愝偑昁梫偲偝傟傞丅
嘇丂岝揹巕専弌偺崅岠棪壔丅杮尋媶偱傢偐偭偨傛偆偵昁偢偟傕崅僄僱儖僊乕暘夝擻傗崅妏搙暘夝擻偼昁
梫偲偟側偄丅
嘊丂椼婲岝丄岝揹巕僄僱儖僊乕丄應掕忦審偺嵟揔壔丅