固体物理学の有名な教科書(C.キッテル著『固体物理学入門、第3版』丸善)の最初は、「原子物理学の一分野としての固体物性の研究は今世紀の初期に始まった。今日では固体物理学は結晶および結晶内の電子状態に関する学問となっている。」という書き出しで始まっている。と言うことで、今回は結晶について少し述べてみましょう。
我々の身の回りの物は、原子の集合体である。それらは、気体、液体、固体の状態で存在している。気体の典型例は、我々が呼吸しているとき吸う「空気」である。液体と言うと、誰でも「水」を、思い浮かべるであろう。それでは、固体というと何を思い浮かべるのであろうか?「氷」でも結構、10円玉の「銅」、アルミサッシの「アルミニウム」、食卓にある「塩(岩塩ともいう)」、等など沢山あります。これらは、「銅」や「アルミニウム」の様に一種類の原子で構成されているもの、「氷」の様に水素と酸素、「岩塩」の様にナトリウムと塩素、と2種類の原子から構成されているもの、更に3種類、4種類と色々あります。
さて、固体を構成する原子は、固体の中ではどうなっているのだろうか。原子が空間的にある規則に従って並んでいるのを結晶と言います。これに対して、部分的に不規則なもの、更には全く乱雑になっているもの等、色々あります。現代の固体物理学は、結晶のみならず乱雑な系まで扱っていますが、ここでは、最も取り扱いが簡単な結晶のことを紹介します。
結晶中では原子は3次元的に周期をもって配列しています。1周期に含まれる原子の数は、アルミニウムの結晶の4個、岩塩の結晶の8個(4分子)のように簡単なものから数十個、数百個の複雑なものまでさまざまである。このような原子の周期的な並びは結晶のもつ重要な性質(対称性と言う)の一つで、周期性とよばれます。
さて、この周期性は、大きく分けると、回転と並進があります。回転とは、結晶中のある点(特定の原子の位置の場合もあるし、中間の場合もある)の回りで回転操作したとき、結晶中のすべての原子がその操作で同種の原子位置に移されることである。つぎに、並進とは、結晶をある方向に一定量だけ平行移動することで、やはりこの並進操作ですべての原子が同種の原子位置に移されることである(この場合、結晶の大きさは無限大と考えています)。このような性質で、3次元の結晶を分類すると、230個のグループに分類されます。

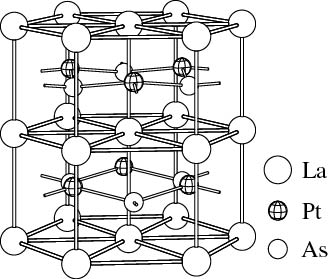
図に、この230分類中186番目の六方晶LiGaGe型LaPtAs結晶の単位格子の透視図を示します。底面中心の大きい白丸(La原子の位置)を中心にして、垂直方向の軸の回りに120度回転するとすべての原子が同種の原子位置に移されることがわかりますね。単位格子と言うのは、これを並進操作で3次元的に繰り返してゆくことで、大きな結晶を表すことができることを意味しています。
さて、結晶の単位格子の大きさは、簡単な結晶では一辺の長さがが3〜5オングストローム(1オングストローム=10の-10乗メートル)程度です。従って、1立方センチメートル(角砂糖1個の大きさ)中には、約10の22乗個の単位格子が存在することになり、この数はアボガドロ定数(6×10の23乗)にほぼ匹敵しますね。よって、上記で、結晶の大きさを無限大と考えることの妥当性が理解できると思います。
このような結晶の、色々な性質(物性といいますが)をその中の電子と原子核の運動として調べるのが固体物理学です。詳細は次回にしますので、御期待ください。
付録.2次元平面のタイル張り
上記では、3次元空間の対称性に触れましたが、より簡単な2次元平面ではどうなるだろうか。例えば、平面全体を埋め尽くす(つまり、タイル張りにする)ことができる正多角形は、正三角形、正方形、正六角形の3種類しかないことは、すぐわかりますね。それでは、2種類以上の正多角形で平面全体を埋め尽くす方法は何通りあるでしょうか?更に、正多角形以外のタイルを使ってもよいとしたら、はたまた、平行移動に関する対称性(並進操作)を持たないタイル張り、つまり、非周期的なタイル張りではどうなるだろうか。英国の数学者ロジャー・ペンローズの見つけた、局所的な五重の対称性をもったタイル張りは、1984年に結晶学者たちが発見した「準結晶」と呼ばれるものに発展していきます。
詳細は、K.デブリン著『数学:パターンの科学』日経サイエンス社の第5章を参照してください。